

Next: 例題
Up: 最小二乗法
Previous: 最小二乗法
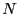 組みのデータ
組みのデータ
![$ (x_i, y_i) [i=1,2,3,\cdots,N]$](img9.png) が与えられたとする.
このとき,各データの組みの直線(一次式)
が与えられたとする.
このとき,各データの組みの直線(一次式)
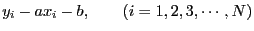 |
(2) |
からのずれが最小となるように,係数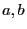 を決定する.
を決定する.
各データについて,式(2)からのずれ(誤差)の2乗の和
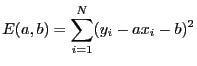 |
(3) |
を自乗誤差と呼ぶ.
自乗誤差は負になることはないので(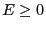 ),
これが最小になるように定数
),
これが最小になるように定数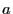 ,
, 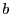 を定める.
を定める.
- 式(3)を最小にする
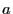 についての条件を求める.
についての条件を求める.
式(3)は,次のように変形できる.
上式は,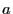 についての2次式であるから,
についての2次式であるから,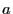 について微分することで
1,
自乗誤差
について微分することで
1,
自乗誤差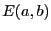 を最小にするための条件が求まる.
結果は次のようになる.
を最小にするための条件が求まる.
結果は次のようになる.
この条件式に,式(3)の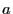 についての偏微分を代入して,
についての偏微分を代入して,
となる.さらに,式を整理すると次式が得られる.
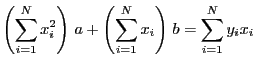 |
(4) |
- 式(3)を最小にするための
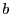 についての条件:
についての条件:
式(3)は
上式を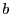 について偏微分して0と置くと,
上の変形と同様にして,条件式が求まる.
について偏微分して0と置くと,
上の変形と同様にして,条件式が求まる.
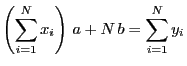 |
(5) |
式(4), (5)を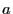 ,
, 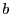 についての
連立1次方程式として解けば,1次式(1)の係数が定まる.
についての
連立1次方程式として解けば,1次式(1)の係数が定まる.


Next: 例題
Up: 最小二乗法
Previous: 最小二乗法
TKinoshita
2016-11-28
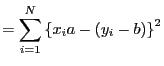
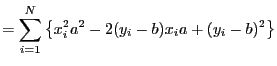
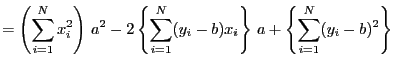
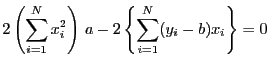
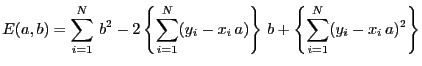
![]() ,
, ![]() についての
連立1次方程式として解けば,1次式(1)の係数が定まる.
についての
連立1次方程式として解けば,1次式(1)の係数が定まる.