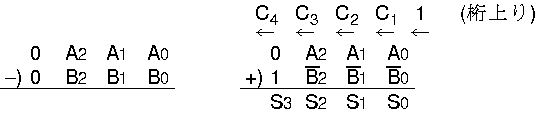- 2進数の加算を行う回路
目次
加算器の構成
半加算器 (Half Adder)
2進数の足し算:
0+0=0, 0+1=1, 1+0=1, 1+1=102
A,Bを入力,C,Sを出力とする2入力2出力,1ビットの加算回路を設計する:
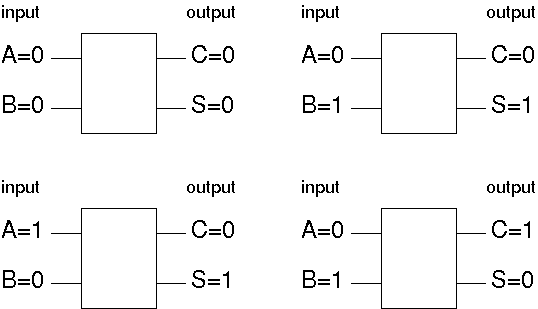
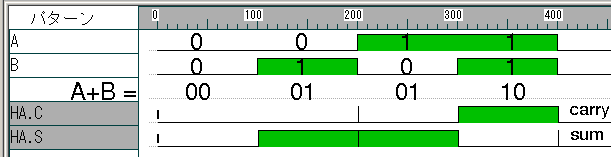
半加算器
A + B = 2×C + S, (A, B, C, S = 0 or 1)
半加算器の真理値表
A B
C
S
0 0
0 0
0 1
0 1
1 0
0 1
1 1
1 0
S: Sum(合計), C: Carry(桁上がり,繰り上がり)
C = A·B
S = A·B + A·B = A⊕B
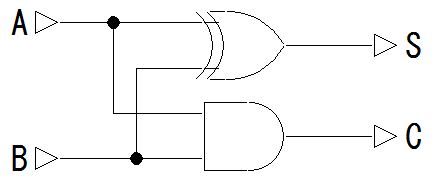
<先頭へ>
全加算器 (Full Adder)
複数桁の加算を行う場合,下の桁からの桁上がりを考慮する必要がある.
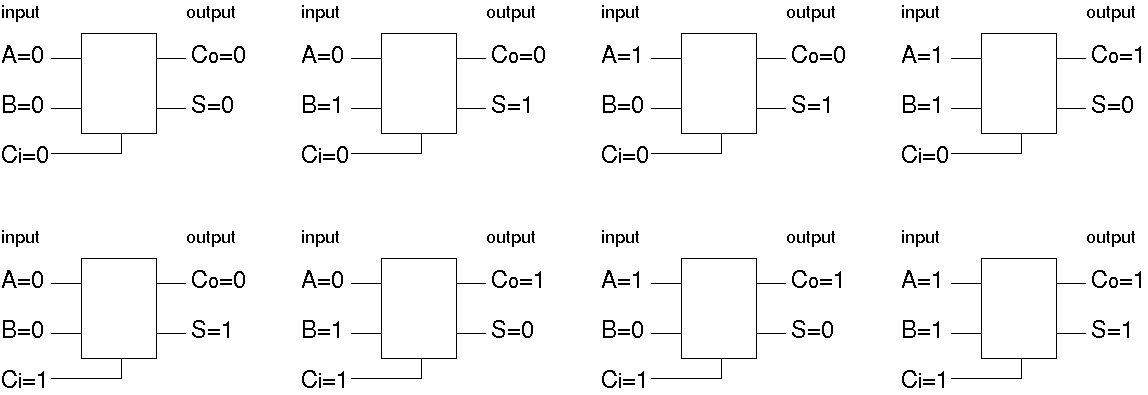
全加算器
全加算器の真理値表
A B
Ci
Co
S
0 0 0
0 0
0 0 1
0 1
0 1 0
0 1
0 1 1
1 0
1 0 0
0 1
1 0 1
1 0
1 1 0
1 0
1 1 1
1 1
C0 = A·B
+ B·C1 + C1·A
S =
A·B·C
+
A·B·C
+
A·B·C
+
A·B·C
=
A·(B·C
+
B·C)
+
A·(B·C
+
B·C)
=
A·(B⊕C)
+
A·(B⊕C)
=
A⊕(B⊕C)
=
A⊕B⊕C
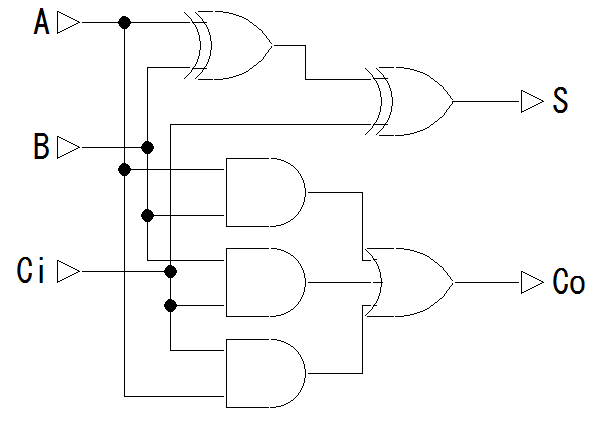
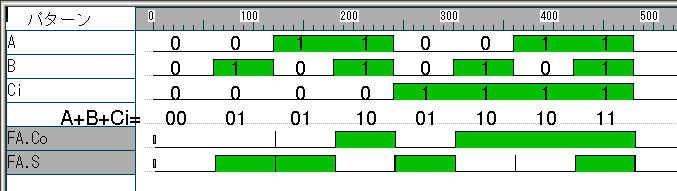
<先頭へ>
半加算器 (Half Adder)
2進数の足し算:

半加算器
S: Sum(合計), C: Carry(桁上がり,繰り上がり)
<先頭へ>
0+0=0, 0+1=1, 1+0=1, 1+1=102
A,Bを入力,C,Sを出力とする2入力2出力,1ビットの加算回路を設計する:

半加算器
A + B = 2×C + S, (A, B, C, S = 0 or 1)
| 半加算器の真理値表 | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
C = A·B
S = A·B + A·B = A⊕B


全加算器 (Full Adder)
複数桁の加算を行う場合,下の桁からの桁上がりを考慮する必要がある.
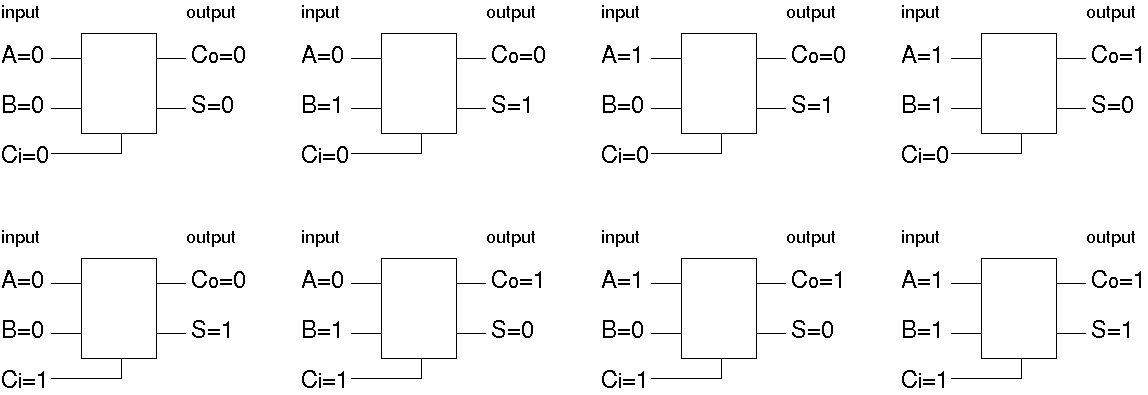
全加算器


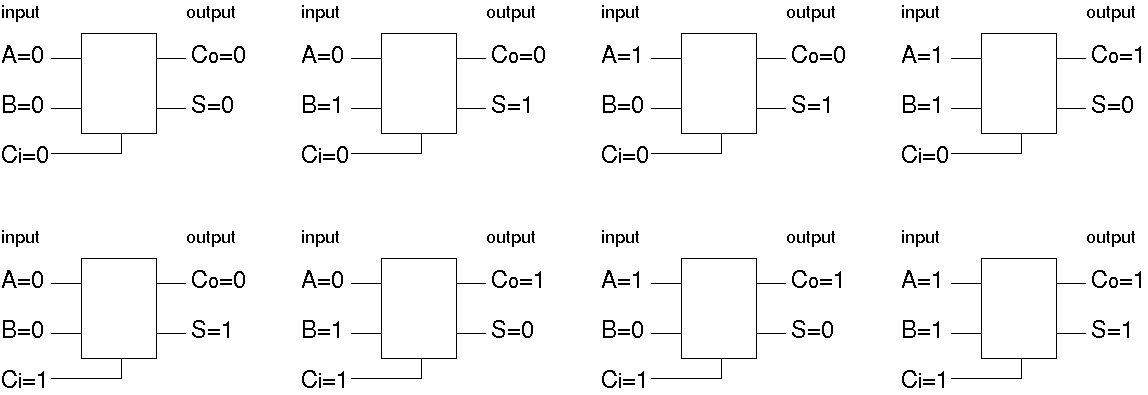
全加算器
| 全加算器の真理値表 | |||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
C0 = A·B + B·C1 + C1·A
S =
A·B·C
+
A·B·C
+
A·B·C
+
A·B·C
=
A·(B·C
+
B·C)
+
A·(B·C
+
B·C)
=
A·(B⊕C)
+
A·(B⊕C)
=
A⊕(B⊕C)
=
A⊕B⊕C


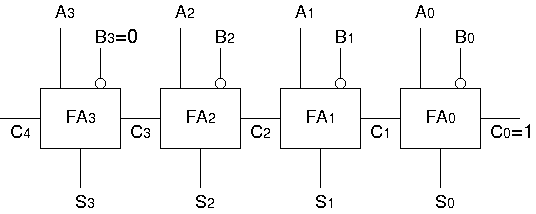
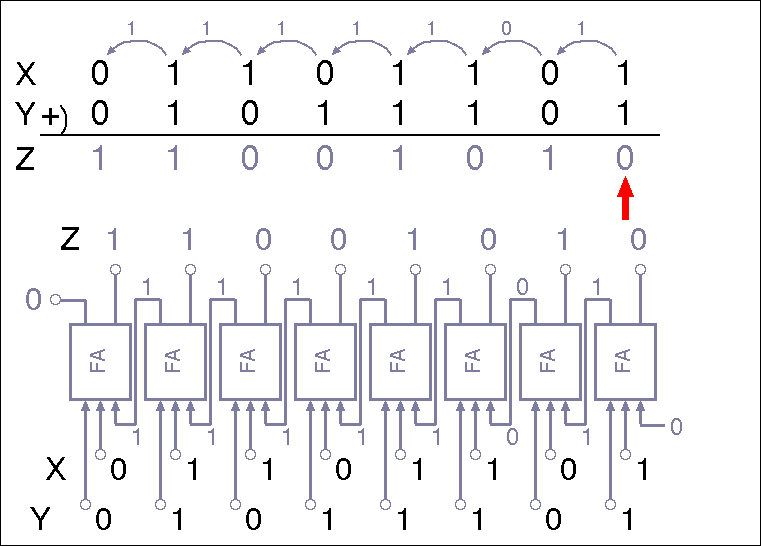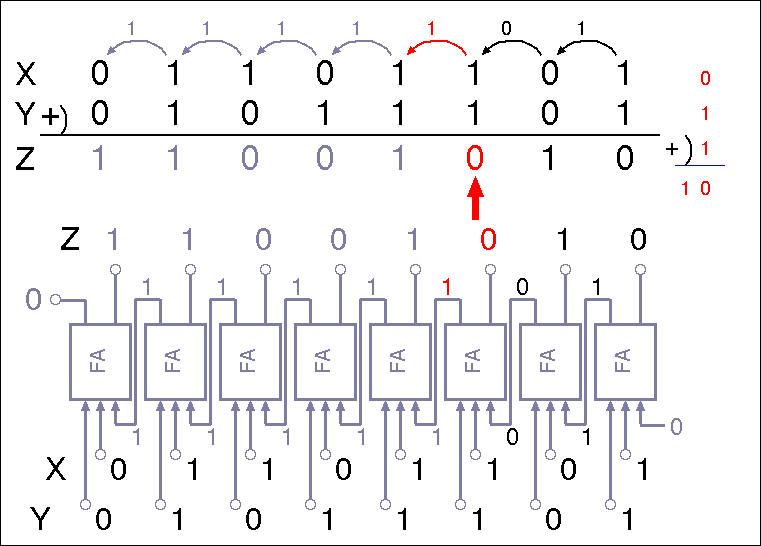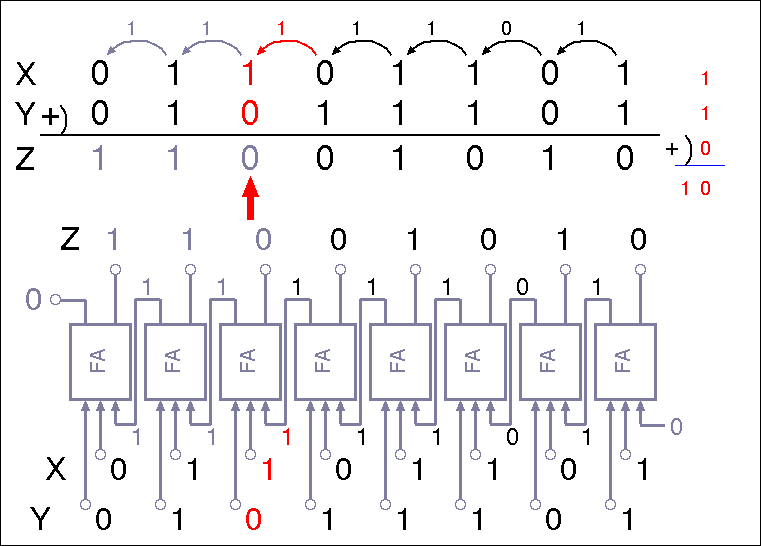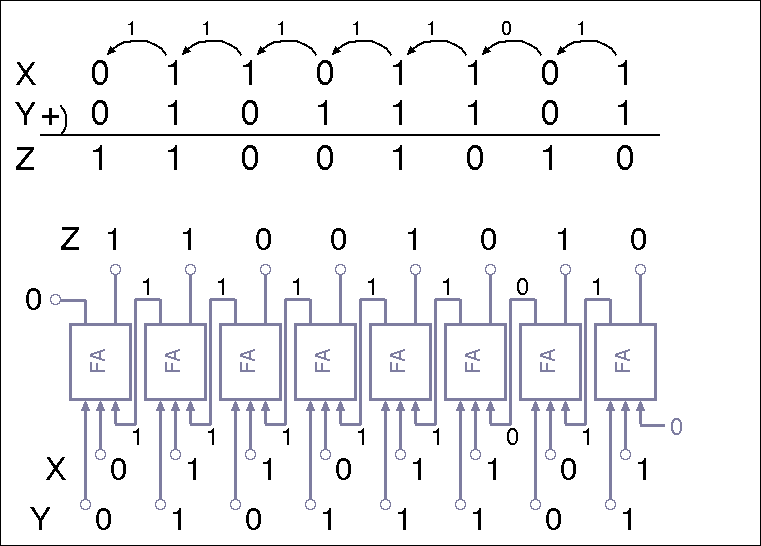
加算回路
1ビットの加算
A + B = (CS)2
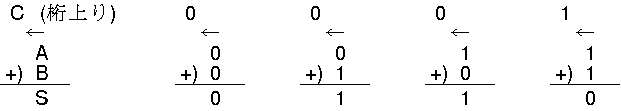
2ビットの加算
(A1 A0)2
+
(B1 B0)2
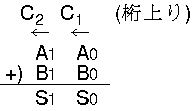
|
|
|---|---|
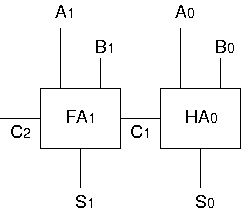
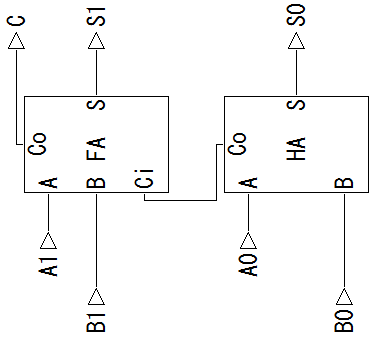
| Full Adder と Half Adder で構成した 2ビット加算回路 | |
|
| |
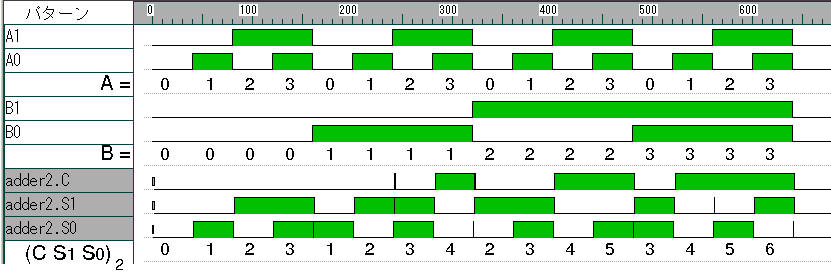
| 2ビット加算回路のタイムチャート | |
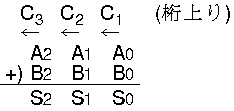
3ビットの加算:
(A2 A1 A0)2
+
(B2 B1 B0)2
|
|---|
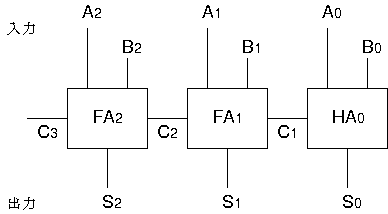
| 3ビット加算器 |