補数
6 + 4 = 10 である.
このとき,4 は 10 に対する 6 の補数であるという.
補数は,余数とも呼ばれる.
補数を用いれば,減算(M - N)を加算(M + [Nの補数])に変換して求めることができる.
→補数を利用した減算の説明
2の補数
コンピュータでは負の整数を表現する際に,補数が使用される.
Nを正の整数とするとき,
負数 -N を2の補数である
2K-N
により表す.
(ただし,0≤N≤2K-1)
[例] 23の補数
| N | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| -N | -1 | -2 | -3 | -4 |
| 補数 | 7 | 6 | 5 | 4 |
| ビット列 | 111 | 110 | 101 | 100 |
3ビットを使って2進数をカウントアップする
000, 001, 010, 011, 100, 101, 110, 111, 000, 001, 010, 011, 100, 101, ...
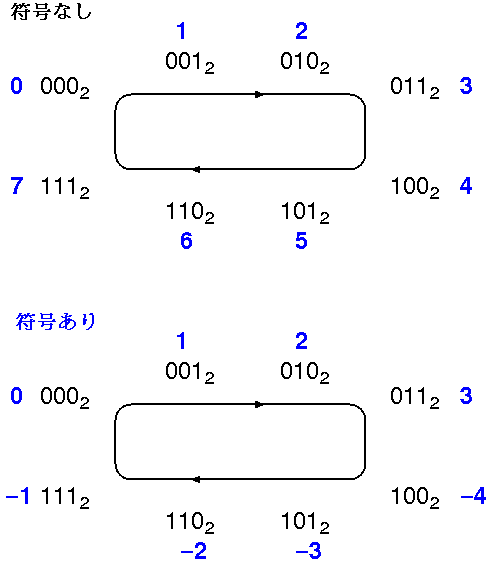
負数の表現に補数を用いると, 次のように数値を割り当てることができ,たし算をする場合に都合がよい。
| ..., | 0002, | 0012, | 0102, | 0112, | 1002, | 1012, | 1102, | 1112, | 0002, | 0012, | 0102, | 0112, | 1002, | 1012, | ... |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
補数を用いた減算 (M-N)
M, N を2進数 K-1 ビットで表される正の整数とする. このとき,0≤N<2K-1, 0≤M<2K-1である.
このMとNの減算,M-Nの補数を利用した計算方法を説明する.
Nに対する2kの補数は,2k - N である,「M」と「Nに対する補数」をたし合わせると,
M + (2K - N) = M - N + 2Kであるから,
- M ≥ N の場合は,2K は桁溢れ分となり, 桁溢れを無視すると,減算値と一致する
- M < N の場合は,加算結果(M-N+2K)の補数を求めると,
2K - (M - N + 2K) = N - M
であるから,減算値の補数と一致する.
なお,この場合は,必ず,M-N+2K > 2K-1 となり, 2進数Kビットで表したときの先頭は1になる.
減算の計算手順 (M - N)
- Mの補数を求める(=M')
- N+M' を計算する(=Y)
- 上記の計算で桁溢れが生じる場合は, 桁溢れを無視したYの値が減算値(N-M)である
- 桁溢れが生じない場合は,計算結果(Y)は負数であり,Yの補数を求め,
マイナス符号を付けたものが減算の結果(N-M)である
例えば,2進数3ビットの場合, 210=0102に対する23(=8)の補数は 6(=8-2)であり,610=1102であるから,
0112 (= 310)
+) 1102 (= -210)
------------------------
10012 桁溢れを無視すると 0012 (= 1)
と桁溢れを無視すれば,正数と同じ手順で加算することができる.
次に,3に対する23(=8)の端数は
510=1012であり,
0102 (= 210)
+) 1012 (= -310)
------------------------
1112 桁溢れなし
桁溢れはないが,先頭ビットが1になっているので,結果は負数である.
補数を計算すると, 8-(111)2=8-7=110であるから,
計算結果は -1 であることがわかる,
符号ビット
先頭(最上位)ビットが
0の場合は正整数,1の場合は負整数を表わす.
これを符号ビットと呼ぶ.
- 符号ビットが0の場合は0または正整数であり, ピットパターンを2進表現と解釈する
- 符号ビットが1の場合は負整数である.
桁溢れを除いて, そのビットパターンに加算したとき結果が0になるよう加える数にマイナス符号(-)を付けた数値を表現する
負整数のビット表現
負の整数を補数により表現する.
負数bの2進数表記の0と1を入れ替えた数をmとすると,
n + m = 11...12であり,これに1を加えて,桁溢れを無視すると
n + m + 1 = 000...0002 = 0であるから
n = -(m+1)なる関係を満足する. このことから,
- n = -{(ビットパターンの0と1を入れ替える) + 1}
m = (-n) - 1 = |n| - 1であるから,
補数への変換操作
- 符号を取り除いた値を2進数で表す
- 先頭に0を追加する
- 各桁の0と1を入れ替える
- 1を加える
負整数の表現(ビットパターン)
次の操作によっても,負整数の表現を求めることができる.
- 符号を取り除いた値を2進数で表す
- 先頭に0を追加する
- 下位の桁から,上位へ向かって次の操作をする
- その桁の値が1であれば,それを1のままにして, 残りの上位のすべての桁の0と1を入れ替える.その後,操作を終える
- その桁の値が0であれば,0のままにして,隣の上位の桁を調べる
[例] -3を4桁の補数で表す.
| (1) | 3を2進数で表す(4ビット) | 0011 |
|---|---|---|
| (2) | 0と1を反転する | 1100 |
| (3) | 1加える | 1100 + 1 = 1101 |
3 = (0001)2 → 1101
[例] -20を8桁の補数で表す.
- 20=101002 であるから,20を8桁の2進数で表記すると 00010100
| (1) | 20を2進数で表す(8ビット) | 00010100 |
|---|---|---|
| (2) | 0と1を反転する | 11101011 |
| (3) | 1加える | 11101011 + 1 = 11101100 |
20 = (00010100)2 → 11101100
[別法]
- 20 = 000101002
- 下位の桁から,順に上位へ向かって調べると,下から3桁目に初めて1が現れる. (00010100)
- 下から4桁目とその上位桁のすべての,0と1を入れ替える. (11101100)
- 以上の操作により -20 = 111011002 が求まる