カルノー図による論理式の簡単化(論理積の論理和形式)

  1. 論理回路の簡単化とカルノー図
  2. 簡単化の手順
  3. 演習問題
<戻る>

論理関数の簡単化とカルノー図

例題6.1

次の式をカルノー図(Karnaugh map)を用いて簡単化する．

     Y = A·B·C + A·B·C + A·B·C + A·B·C + A·B·C

  • 真理値表
    真理値表
    入力 出力
    A B C Y
    0000
    0010
    010 1
    0111
    1001
    1010
    1101
    1111
  • カルノー図
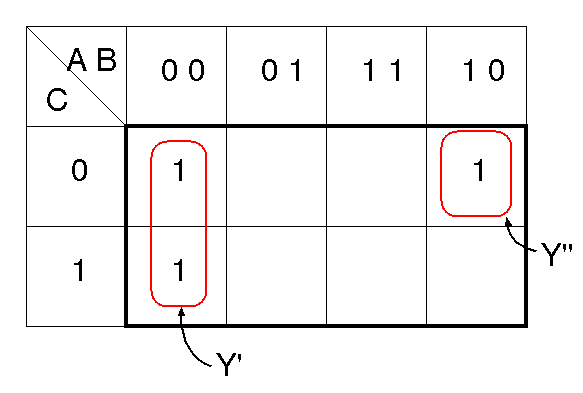
    論理関数Yに対するカルノー図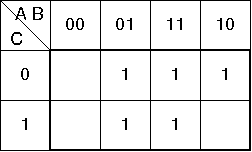
[注意]
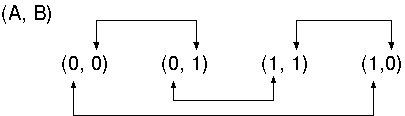
  • (A, B) は隣合う値が1つだけ異なるように配置する
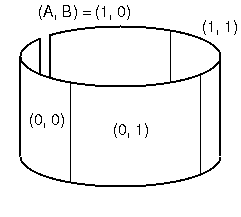
  • 下図の円筒のように考え，切り取って平面に広げ，表にする．
  • ここでは，(0,0)と(1,0)の間で切り離しているが， 任意の境界線で切り離すことができる

    • <先頭へ>

    簡単化の原理と手順

    1. 加法標準形の各最小項に対応するマス目に1を記入する
    2. 1が記入されている隣合う2N個ずつをできるだけ大きな１つのグループに分ける


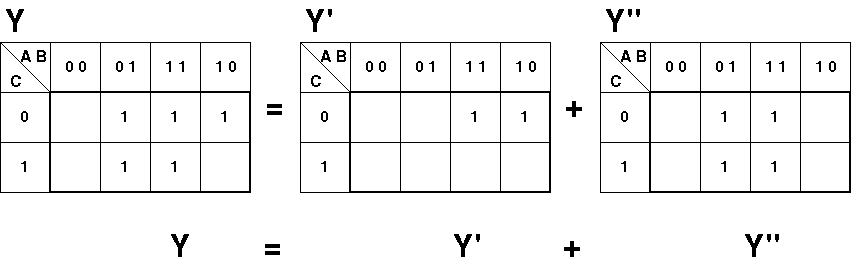
      表中の空欄は0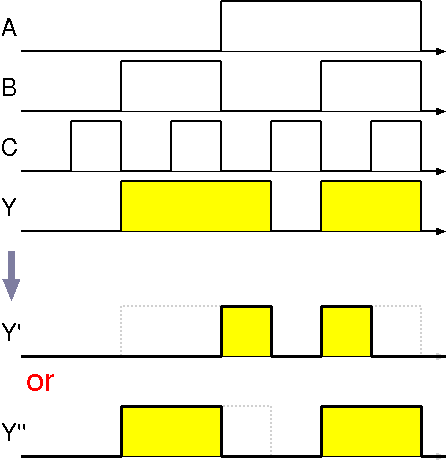

    3. 各グループの論理式を求める

      • Y' = A·B·C + A·B·C に対する簡単化

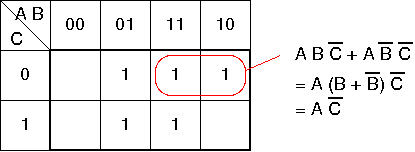
        • 隣合うマスでの値が1つだけ異なるように配置したため，Bだけが異なる．

          Y' =  A·B·C +A·B·C  =  A(B+B)C  =  A·C

      • Y'' = A·B·C + A·B·C + A·B·C + A·B·C に対する簡単化

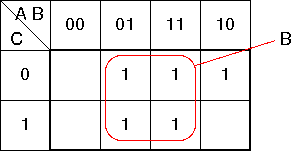
          Y''  =  A·B·C + A·B·C + A·B·C + A·B·C  =  (A+A)·B ·C + (A+A) ·B·C  =  B·C +B·C  =  B·(C+C)  =  B

    4. 得られたすべてのグループを表す論理式の論理和を取る

          Y = Y' + Y'' = A·C + B

    例題２

            Y = A·B·C + A·B·C + A·B·C
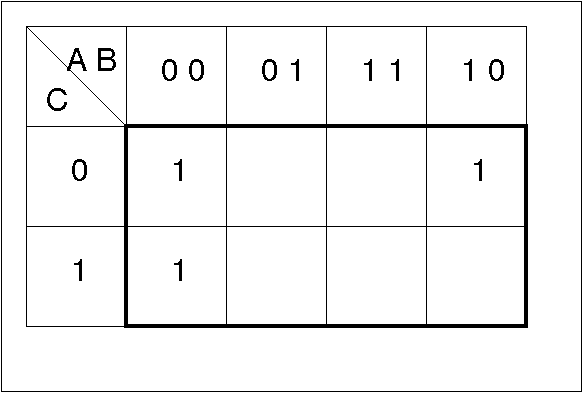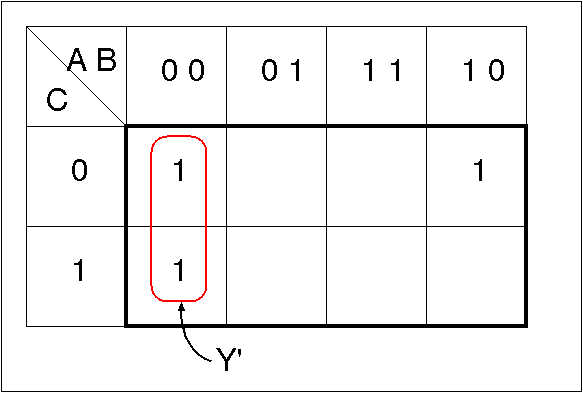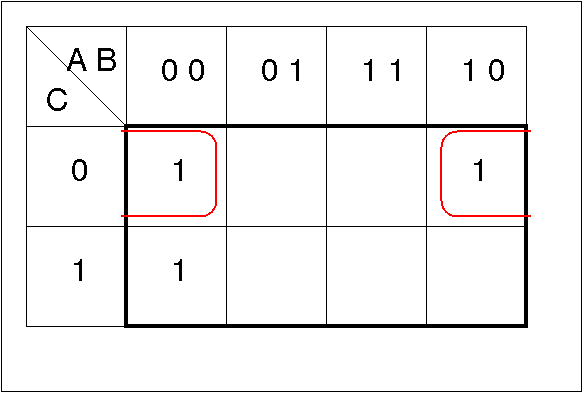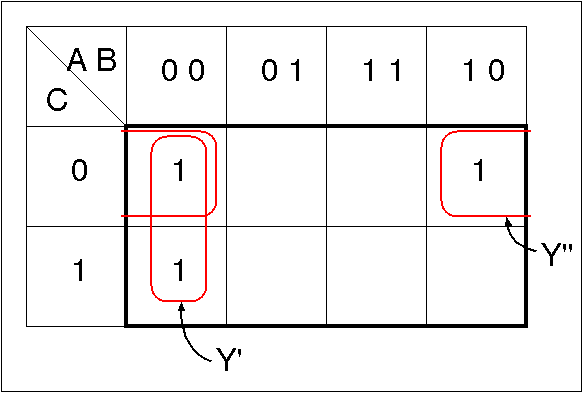
    1. カルノー図を描く

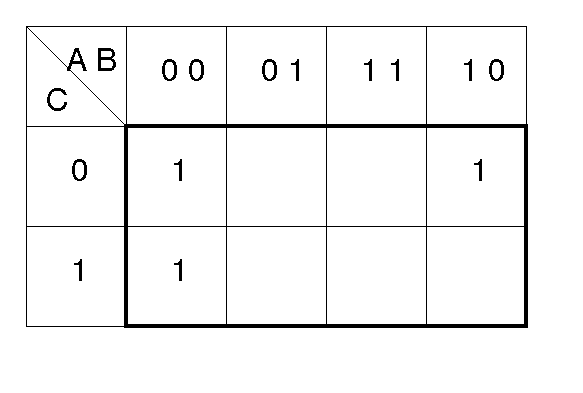
    2. 「1」の枠をグループに分ける

    3. 各グループから論理式を求める 
            Y'  = A·B  [ = A·B·C + A·B·C = A·B·(C + C) ]
      Y'' = B·C  [ = A·B·C + A·B·C = (A + A)·B·C ]
      したがって， 
            Y   = Y' + Y'' = A·B + B·C
    • 上式は，さらに，簡単化することができ， 
            Y = (A + C)·B
      とまとめることができる． カルノー図を使って得られた論理式が， 最も簡単化されたものとは限らないことに注意する必要がある．

    注意

    次のようにグループを分けると，

    得られる論理式は 
          Y'  = A·B
      Y'' = A·B·C
      Y   = A·B +  A·B·C
    となり， Y'' = A·B·C であり，先に求めた B·Cと比べて，簡単化されていない．
    • グループ分けは，重複してでも，できるだけ大きなグループにする

    4入力回路

    <例 2> (ここへ)

    <例 3>

    <先頭へ>

    演習問題

    教科書 p.40 [1], [2]

    2時限目

    p.40の演習問題[1]

      設問(1)に示された論理式と これをカルノー図を用いて簡単化した式の両方を論理回路で表し，
      シミュレータを用いて同じ動作をすることを確認せよ．

    p.40の演習問題[2]

      設問(2)に示された論理式と これをカルノー図を用いて簡単化した式の両方を論理回路で表し，
      シミュレータを用いて同じ動作をすることを確認せよ．

    達成目標

    <戻る>