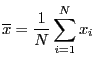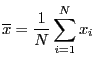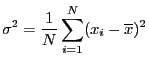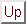

Next: 例題
Up: kadai
Previous: 演習問題(1)
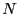 個の数値データ
個の数値データ
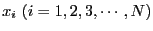 に対する
平均値を
に対する
平均値を
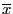 と表すと,
と表すと,
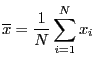 |
(11) |
と定義できる.
各値の平均値からのずれ
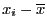 を2乗して,平均値を取ると
を2乗して,平均値を取ると
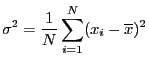 |
(12) |
が定義できる.
この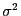 を
を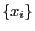 の分散と呼び,
の分散と呼び,
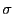 を標準偏差と呼ぶ.
2乗の和であることから,右辺は,かならず,0,または,正の値になる.
さらに,
を標準偏差と呼ぶ.
2乗の和であることから,右辺は,かならず,0,または,正の値になる.
さらに,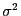 が0となるのは,
が0となるのは,
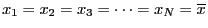 の場合に限られる.
また,平均値からのずれが大きなデータが多数存在すると,
の場合に限られる.
また,平均値からのずれが大きなデータが多数存在すると,
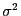 は大きな値になるので,
は大きな値になるので,
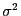 は
は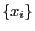 のばらつきを表している.
のばらつきを表している.
Subsections
TKinoshita
2016-11-28