関数 y = x1/2
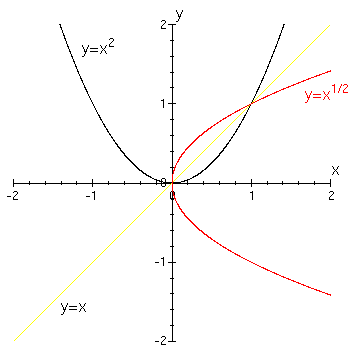２つの関数
y = x2
y = x1/2
は互いに逆関数である。
これらの関数を左図に示す。
グラフは y=x に関して互いに対称に描かれる。
n を正の数、m=n2 とすると
(±n)2 = n2 = m
であるから、
y = x1/2
は、 x=m のとき y = ±n となり、正負の２つの値を取る。
このように、関数
y = f(x)
が、x=a に対して、複数の f(a) の値を持つとき、
f(x) は多価関数であると言う。
上のグラフは x≧0 のときに、 y = x1/2 が正と負の２値を
持つことを示す。
この関数の定義域を複素数に拡張した場合を下の２つの図で表す。
-
"clear : "の右側のボタンをマウスでクリックすると2つの複素平面が描かれる。
w = z1/2
するとき、
左側が複素 z 平面、右側が複素 w 平面を表す。
-
z 平面上でマウスボタンをクリックし、
ボタンを押した状態でマウスポインタを移動する（ドラッグする）と、
その軌跡が描かれる。
-
w 平面には、z1/2の軌跡が同時に描かれる。
-
極形式で表すと、
z = r exp(jθ)
w = r1/2 exp(jθ/2)
であるから、z平面上の点の偏角に対して、
対応するw平面上の点の偏角は 1/2 倍になる。
z平面上のある点を出発して、もとの点に戻るとき、
その軌跡が描く領域内に原点が含まれない場合には、
w平面上の点も出発点に戻る。
しかし、z平面上の軌跡が原点を含む場合には、
w平面での軌跡は出発点へは戻らない。
終点は、出発点に対して位相が 180°異なる、原点を挟んだ反対側の点となる。
原点 z=0 を２周まわることにより、w平面上での対応する点はもとの場所に戻る。
このような、1対1対応ができない不便さを解消する方法として、 Riemann 面と
呼ばれる複素平面の拡張方法があるがここでは述べない。