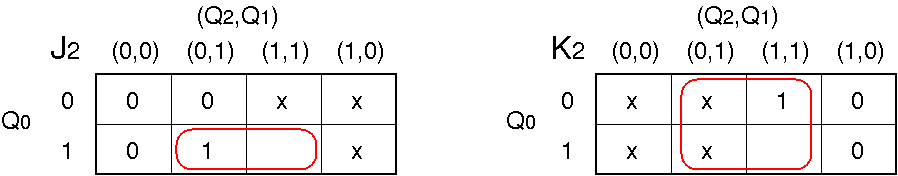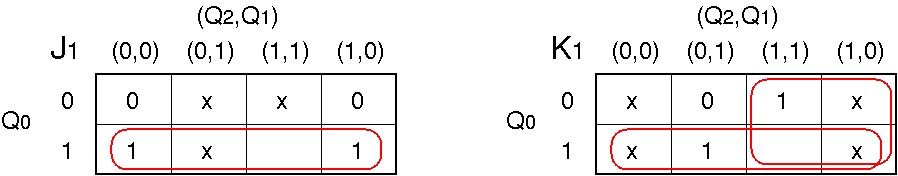同期式順序回路(1), (2)
-
JKフリップフロップの動作特性(復習)
-
3進カウンタ
-
7進カウンタの設計
-
11進カウンタの設計
-
n進カウンタの設計方針
クロック信号(CK)に同期して動作する順序回路
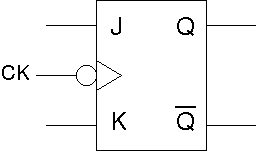
JKフリップフロップ
JKフリップフロップの動作
|
|
|
CK |
J |
K |
Q' |
 |
0 |
0 |
Q |
(hold) |
|
| 0 |
1 |
0 |
(reset) |
| 1 |
0 |
1 |
(set) |
| 1 |
1 |
Q |
(toggle) |
|
それ以外 |
*
|
* |
Q |
(hold) |
|
*
: 0でも1でもよい.
|
|
|
記号
|
|
特性表
|
|
ネガティブエッジ型JKフリップフロップ
|
|---|
- (J,K)=(0,0): 保持動作(hold)
- (J,K)=(1,0): セット動作(set)
- (J,K)=(0,1): リセット動作(reset)
- (J,K)=(1,1): 反転動作(トグル, toggle)
| 状態 |
CK動作後 |
Qn |
J |
K |
Qn+1 |
| 0 |
0 |
0 |
0 |
| 0 |
0 |
1 |
0 |
| 0 |
1 |
0 |
1 |
| 0 |
1 |
1 |
1 |
| 1 |
0 |
0 |
1 |
| 1 |
0 |
1 |
0 |
| 1 |
1 |
0 |
1 |
| 1 |
1 |
1 |
0 |
|
|
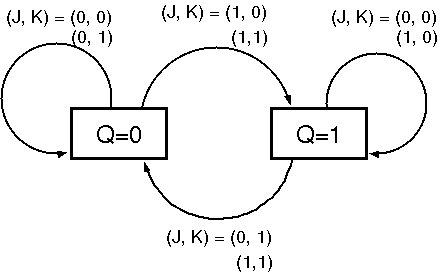
JKフリップフロップの状態遷移図
|
左上の表は次のように書き換えることができる.
| 状態 |
CK動作後 |
Qn |
J |
K |
Qn+1 |
| 0 |
0 |
× |
0 |
| 0 |
1 |
× |
1 |
| 1 |
× |
0 |
1 |
| 1 |
× |
1 |
0 |
|
|
|
Q=0の状態で,J=0を入力すると,Q=0を保持する
|
|---|
|
Q=0の状態で,J=1を入力すると,Q=1に遷移する
|
|---|
|
Q=1の状態で,K=0を入力すると,Q=1を保持する
|
|---|
|
Q=1の状態で,K=1を入力すると,Q=0に遷移する
|
|---|
|
JKフリップフロップの動作特性
-
Q=0の状態で,J=0を入力すると,Q=0を保持する
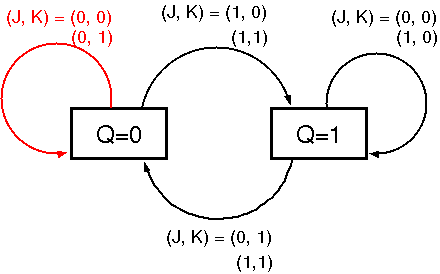
-
Q=0の状態で,J=1を入力すると,Q=1に遷移する
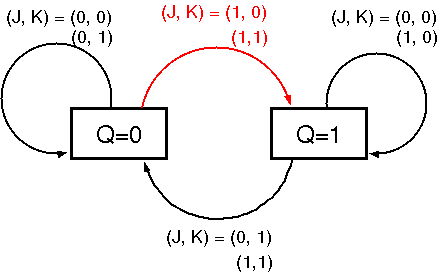
-
Q=1の状態で,K=0を入力すると,Q=1を保持する
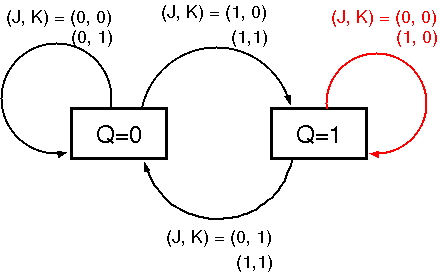
-
Q=1の状態で,K=1を入力すると,Q=0に遷移する
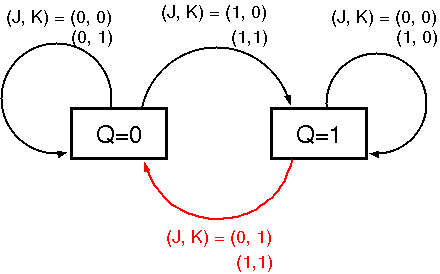
このJKフリップフロップの特性は次の表にまとめることができる.
| 入力 |
状態の変化 |
J |
K |
Qn → Qn+1 |
| 0 |
× |
0 → 0 |
| 1 |
× |
0 → 1 |
| × |
0 |
1 → 1 |
| × |
1 |
1 → 0 |
表中の × は,0, 1 のどちらでも構わないことを表す。
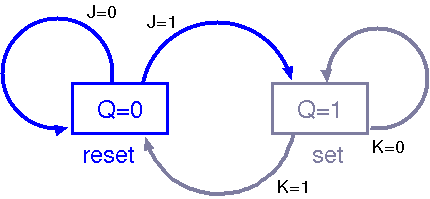
|
Q: 0 → 0
|
Q = 0 の状態で,
J = 0 を入力するとセットされない
|
|
Q: 0 → 1
|
Q = 0 の状態で,
J = 1 を入力するとセットされる
|
|
Q: 1 → 1
|
Q = 1 の状態で,
K = 0 を入力するとリセットされない
|
|
Q: 1 → 0
|
Q = 1 の状態で,
K = 1 を入力するとリセットされる
|
3進カウンタ
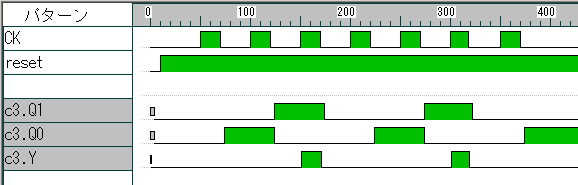
クロックパルスが3つ入るたびに,3つ目の入力に同期して1を出力する回路を設計する.
下図に示すCKはクロック信号,Yは出力信号である.
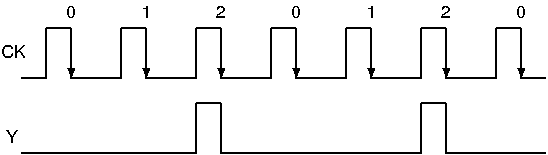
3進カウンタのタイムチャート
これを実現するには,少なくとも3つの状態を持つ順序回路が必要に鳴る.
ここでは,2つのJKフリップフロップを使用する.
フリップフロップ FF0, FF1の各出力を
Q1, Q0と表し,
(Q1, Q0) = (0, 0), (0, 1), (1, 0)
の3つの状態を利用する.
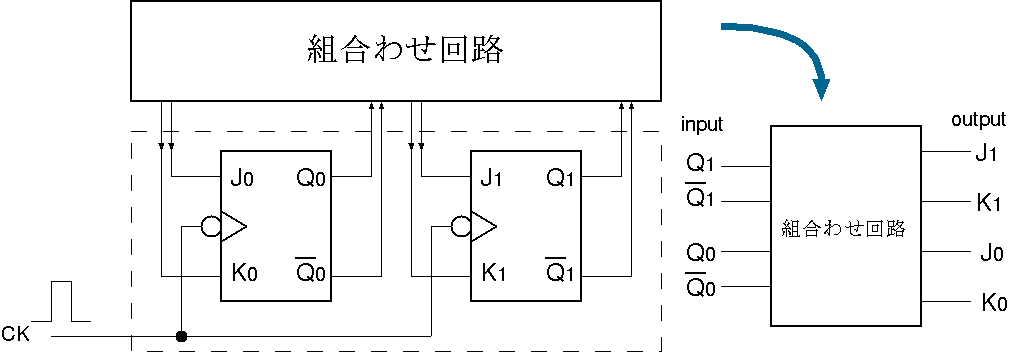
J, K端子への入力信号
カウンタ動作に要求される J, K入力の値
- クロックパルスに同期して,n = 0, 1, 2, 0, 1, 2, 0, ... と変化を繰り返す
- nでの各JKクリップフロップの出力を
Q1n, Q0n
と表す
- クロックパルスの立ち下がり直後のフリップフロップの出力を
Q1n+1, Q0n+1
と表す
- n=2の次は,n=0に戻ることに注意して3進カウンタの状態の遷移を調べる
クロックパルス立ち下がり前後での状態の遷移
- n=0から1への遷移とそのための J, Kへの入力信号
- (Q1, Q0) = (0, 0) から (0, 1) へ
- Q1は 0 から 0 へ(リセット状態を保持する)
- この動作のための入力は,
(J1, K1)=(0,×)
- Q0は 0 から 1 へ(セット状態へ遷移する)
- この動作のための入力は,
(J0, K0)=(1,×)
n=0から1への状態の変化とそのためのJ, K への入力
|
(Q1, Q0)の状態
|
クロック信号の立ち下がり前後での状態の変化
|
各J, K端子への入力
|
|
n
|
Q1n
|
Q0n
|
Q1n → Q1n+1
|
Q0n → Q0n+1
|
J1 |
K1 |
J0 |
K0 |
| 0 |
0 |
0 |
0 → 0 (hole) |
0 → 1 (set) |
0 |
× |
1 |
× |
× は 0, 1 のどちらでも構わないことを表す
- 同様にして,
- n=1から2への遷移とそのための J,Kへの入力信号を求める
- n=2から0への遷移とそのための J,Kへの入力信号を求める
以上により得られる,3進カウンタの動作とJ, K端子への入力信号を下表に示す.
3進カウンタの動作表
|
(Q1, Q0)の状態
|
クロック信号の立ち下がり前後での状態の変化
|
各J, K端子への入力
|
|
n
|
Q1n
|
Q0n
|
Q1n → Q1n+1
|
Q0n → Q0n+1
|
J1 |
K1 |
J0 |
K0 |
| 0 |
0 |
0 |
0 → 0 (hold) |
0 → 1 (set) |
0 |
× |
1 |
× |
| 1 |
0 |
1 |
0 → 1 (set) |
1 → 0 (reset) |
1 |
× |
× |
1 |
| 2 |
1 |
0 |
1 → 0 (reset) |
0 → 0 (hold) |
× |
1 |
0 |
× |
× は 0, 1 のどちらでも構わないことを表す
表の説明
- 1列目(n): 順に入力するクロック信号の番号
- 2列目: (Q1, Q0) の値
- 3列目: クロック信号の立ち下がり前後での出力値の変化
- 4列目: 出力変化のために要求される (J, K)の値
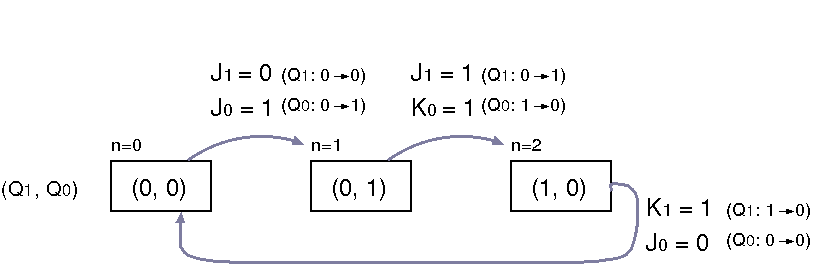
3進カウンタの状態の遷移
J1, K1 への入力信号
上の3進カウンタの動作表の
Q
1n, Q
0n,
J
1, K
1の列
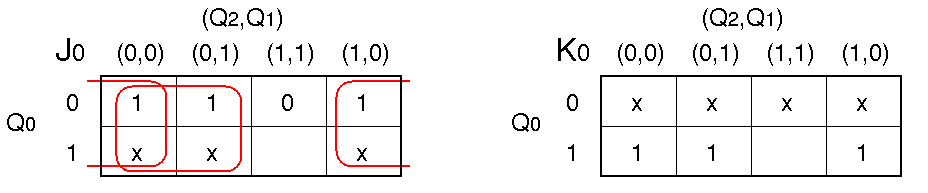
より,次の真理値表(下図左側)が得られる.
さらに,右側のカルノー図が得られる:
真理値表
| Q1n |
Q0n |
J1 |
K1 |
| 0 | 0 | 0 | × |
| 0 | 1 | 1 | × |
| 1 | 0 | × | 1 |
|
|
カルノー図
| |
|---|
| J1 |
Q1=0 |
Q1=1 |
| Q0=0 |
0 |
× |
Q0=1 |
1 |
|
|
|
|
| K1 |
Q1=0 |
Q1=1 |
| Q0=0 |
× |
1 |
Q0=1 |
× |
|
|
|
空欄は未定義項
|
|
カルノー図を利用して,J
1, K
1
へ入力する信号を Q
1, Q
0 の論理式で表すことができる:
J1 = Q0, K1 = Q0
J0, K0 への入力信号
同様に,上の3進カウンタの動作表より,次の真理地表とカルノー図が得られる:
真理値表
| Q1n |
Q0n |
J0 |
K0 |
| 0 | 0 | 1 | × |
| 0 | 1 | × | 1 |
| 1 | 0 | 0 | × |
|
|
カルノー図
| |
|---|
| J0 |
Q1=0 |
Q1=1 |
| Q0=0 |
1 |
0 |
Q0=1 |
× |
|
|
|
|
| K0 |
Q1=0 |
Q1=1 |
| Q0=0 |
× |
× |
Q0=1 |
1 |
|
|
|
空欄は未定義項
|
|
J0 = Q1, K0 = Q1
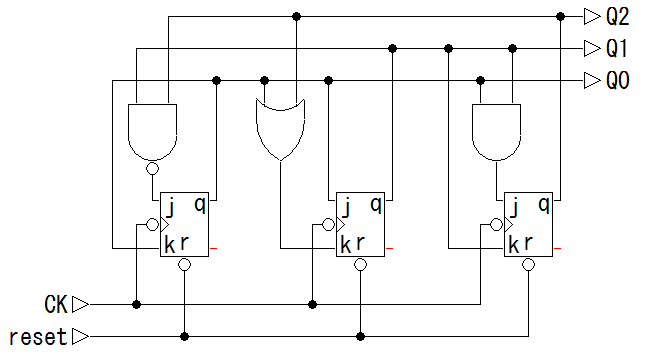
以上より,
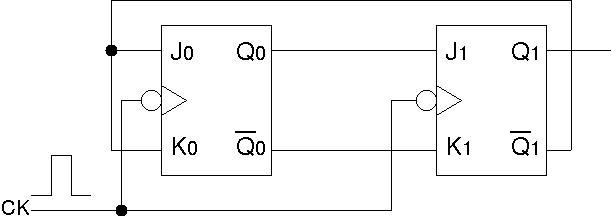
J0 = K0 = Q1, J1 = Q0, K1 = Q0
が得られる.
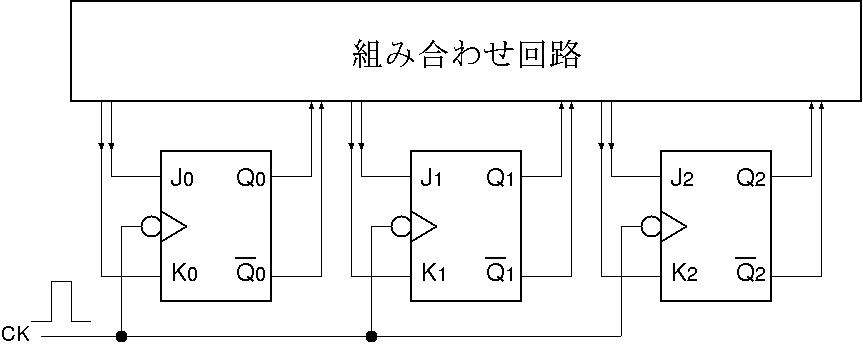
この式に従って結線した回路図を以下に示す.
シミュレーション:
7進カウンタ
- 0〜6まで7つの状態を持つので3ビットが必要である
- JKフリップフロップを3段使用し,7進カウンタとして動作するように
組み合わせ回路を設計する
| n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
| 2進表現 |
0000 |
0001 |
0010 |
0011 |
0100 |
0101 |
0110 |
各フリップフロップに要求される状態の変化を下表に示す.
7進カウンタの状態の変化
| n |
フリップフロップの状態 |
n+1 |
n+1 での状態 |
状態の変化 |
| Q2n |
Q1n |
Q0n |
Q2n+1 |
Q1n+1 |
Q0n+1 |
Q2n
→ Q2n+1 |
Q1n
→ Q1n+1 |
Q0n
→ Q0n+1 |
| 0 |
0 |
0
| 0 |
1 |
0 |
0 |
0 |
0 → 0 |
0 → 0 |
0 → 1 |
| 1 |
0 | 0 | 1 |
2 |
0 |
1 |
0 |
0 → 0 |
0 → 1 |
1 → 0 |
| 2 |
0 | 1 | 0 |
3 |
0 |
1 |
1 |
0 → 0 |
1 → 1 |
0 → 1 |
| 3 |
0 | 1 | 1 |
4 |
1 |
0 |
0 |
0 → 1 |
1 → 0 |
1 → 0 |
| 4 |
1 | 0 | 0 |
5 |
1 |
0 |
1 |
1 → 1 |
0 → 0 |
0 → 1 |
| 5 |
1 | 0 | 1 |
6 |
1 |
1 |
0 |
1 → 1 |
0 → 1 |
1 → 0 |
| 6 |
1 | 1 | 0 |
0 |
0 |
0 |
0 |
1 → 0 |
1 → 0 |
0 → 0 |
- 7進カウンタであるから,n = 0, 1, 2, ..., 5, 6 と変化して次は0に戻る
-
JKフリップフロップの特性から,
上の動作をするためのJK端子への入力値が定まる.
7進カウンタの状態の変化と J, Kへの入力
| n |
フリップフロップの状態 |
状態の変化と (J, K)への入力値 |
| Q2n |
Q1n |
Q0n |
Q2n
→ Q2n+1 |
(J2, K2) |
Q1n
→ Q1n+1 |
(J1, K1) |
Q0n
→ Q0n+1 |
(J0>, K0) |
| 0 |
0
| 0
| 0 |
0 → 0 |
(0, ×) |
0 → 0 |
(0, ×) |
0 → 1 |
(1, ×) |
| 1 |
0 | 0 | 1 |
0 → 0 |
(0, ×) |
0 → 1 |
(1, ×) |
1 → 0 |
(×, 1) |
| 2 |
0 | 1 | 0 |
0 → 0 |
(0, ×) |
1 → 1 |
(×, 0) |
0 → 1 |
(1, ×) |
| 3 |
0 | 1 | 1 |
0 → 1 |
(1, ×) |
1 → 0 |
(×, 1) |
1 → 0 |
(×, 1) |
| 4 |
1 | 0 | 0 |
1 → 1 |
(×, 0) |
0 → 0 |
(0, ×) |
0 → 1 |
(1, ×) |
| 5 |
1 | 0 | 1 |
1 → 1 |
(×, 0) |
0 → 1 |
(1, ×) |
1 → 0 |
(×, 1) |
| 6 |
1 | 1 | 0 |
1 → 0 |
(×, 1) |
1 → 0 |
(×, 1) |
0 → 0 |
(0, ×) |
- J2と K2の決定
上の表から,Q2n, Q1n,
Q0, J2 (K2)の列だけを取り出す:
| Q2n |
Q1n |
Q0n |
J2 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | × |
| 1 | 0 | 1 | × |
| 1 | 1 | 0 | × |
| |
| Q2n |
Q1n |
Q0n |
K2 |
| 0 | 0 | 0 | × |
| 0 | 0 | 1 | × |
| 0 | 1 | 0 | × |
| 0 | 1 | 1 | × |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
|
|---|
カルノー図を利用して,J2 (K2) を
Q2, Q1, Q0 の論理式で表すことができる.
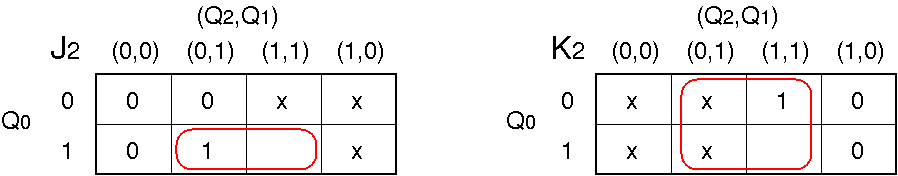
J2 = Q1·Q0,
K2 = Q1
- (J1, K1)の決定
(J2, K2)の場合と同様に
7進カウンタの状態の変化と J, K への入力の表から,
Q2n, Q1n,
Q0, J1,
K1の列だけを取り出す:
| Q2n |
Q1n |
Q0n |
J1 |
K1 |
| 0 | 0 | 0 | 0 | × |
| 0 | 0 | 1 | 1 | × |
| 0 | 1 | 0 | × | 0 |
| 0 | 1 | 1 | × | 1 |
| 1 | 0 | 0 | 0 | × |
| 1 | 0 | 1 | 1 | × |
| 1 | 1 | 0 | × | 1 |
カルノー図を利用して,J1, K1 を
Q2, Q1, Q0 の論理式で表す.
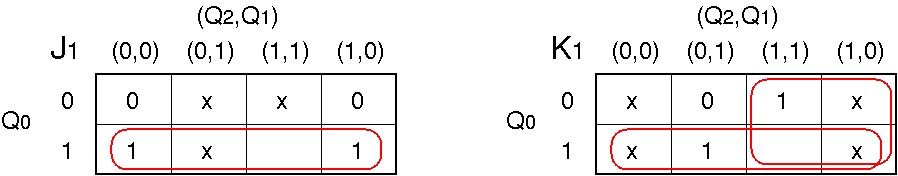
J
1 = Q
0,
K
1 = Q
2 + Q
0
- (J0, K0)の決定
同様に,
7進カウンタの状態の変化と J, K への入力の表から,
Q2n, Q1n,
Q0, J0,K0の列だけを取り出す:
| Q2n |
Q1n |
Q0n |
J0 |
K0 |
| 0 | 0 | 0 | 1 | × |
| 0 | 0 | 1 | × | 1 |
| 0 | 1 | 0 | 1 | × |
| 0 | 1 | 1 | × | 1 |
| 1 | 0 | 0 | 1 | × |
| 1 | 0 | 1 | × | 1 |
| 1 | 1 | 0 | 0 | × |
カルノー図を利用して,J0, K0 を
Q2, Q1, Q0 の論理式で表す.
J0 = Q2
+ Q1
= Q2·
Q1,
K0 = 1 (あるいは K0 = Q0)
J0 = Q2·
Q1,
K0 = Q0
J1 = Q0,
K1 = Q2 + Q0
J2 = Q1·Q0,
K2 = Q1
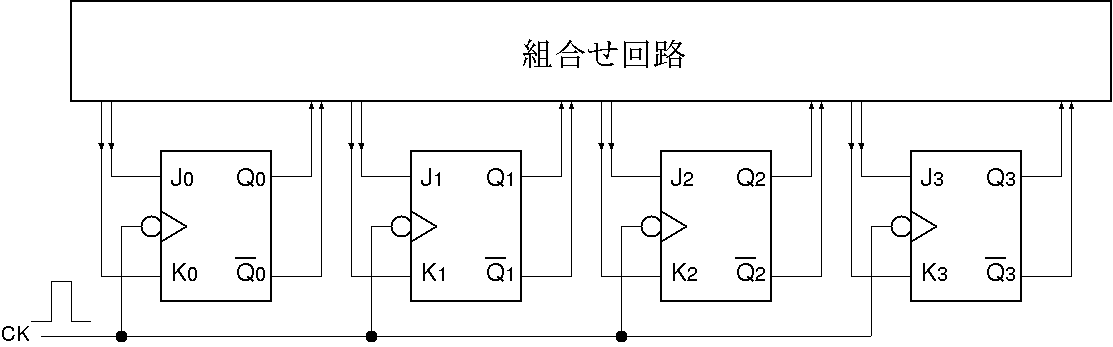
11進カウンタ
- 4ビットが必要である
- JKフリップフロップを4段使用し,11進カウンタとして動作するように
組み合わせ回路を設計する
- (J, K)端子への入力信号とQ3, Q2, Q1,
Q0 の関係をカルノー図を利用して論理式で表す
| n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 2進表現 |
0000 |
0001 |
0010 |
0011 |
0100 |
0101 |
0110 |
0111 |
1000 |
1001 |
1010 |
各フリップフロップに要求される状態の変化を下表に示す.
11進カウンタの状態の変化
| n |
フリップフロップの状態 |
n+1 |
n+1 での状態 |
状態の変化 |
| Q3n |
Q2n |
Q1n |
Q0n |
Q3n+1 |
Q2n+1 |
Q1n+1 |
Q0n+1 |
Q3n
→ Q3n+1 |
Q2n
→ Q2n+1 |
Q1n
→ Q1n+1 |
Q0n
→ Q0n+1 |
| 0 |
0 |
0 |
0
| 0 |
1 |
0 |
0 |
0 |
1 |
0 →
0 |
0 →
0 |
0 →
0 |
0 →
1 |
| 1 |
0 | 0 | 0 | 1 |
2 |
0 |
0 |
1 |
0 |
0 →
0 |
0 →
0 |
0 →
1 |
1 →
0 |
| 2 |
0 | 0 | 1 | 0 |
3 |
0 |
0 |
1 |
1 |
0 →
0 |
0 →
0 |
1 →
1 |
0 →
1 |
| 3 |
0 | 0 | 1 | 1 |
4 |
0 |
1 |
0 |
0 |
0 →
0 |
0 →
1 |
1 →
0 |
1 →
0 |
| 4 |
0 | 1 | 0 | 0 |
5 |
0 |
1 |
0 |
1 |
0 →
0 |
1 →
1 |
0 →
0 |
0 →
1 |
| 5 |
0 | 1 | 0 | 1 |
6 |
0 |
1 |
1 |
0 |
0 →
0 |
1 →
1 |
0 →
1 |
1 →
0 |
| 6 |
0 | 1 | 1 | 0 |
7 |
0 |
1 |
1 |
1 |
0 →
0 |
1 →
1 |
1 →
1 |
0 →
1 |
| 7 |
0 | 1 | 1 | 1 |
8 |
1 |
0 |
0 |
0 |
0 →
1 |
1 →
0 |
1 →
0 |
1 →
0 |
| 8 |
1 | 0 | 0 | 0 |
9 |
1 |
0 |
0 |
1 |
1 →
1 |
0 →
0 |
0 →
0 |
0 →
1 |
| 9 |
1 | 0 | 0 | 1 |
10 |
1 |
0 |
1 |
0 |
1 →
1 |
0 →
0 |
0 →
1 |
1 →
0 |
| 10 |
1 | 0 | 1 | 0 |
0 |
0 |
0 |
0 |
0 |
1 →
0 |
0 →
0 |
1 →
0 |
0 →
0 |
JKフリップフロップの特性から,
上の動作をするためのJK端子への入力値が定まる.
11進カウンタの状態の変化と(J, K)への入力値
| n |
フリップフロップの状態 |
状態の変化と(J, K)への入力値 |
| Q3n |
Q2n |
Q1n |
Q0n |
Q3n
→ Q3n+1 |
(J3, K3) |
Q2n
→ Q2n+1 |
(J2, K2) |
Q1n
→ Q1n+1 |
(J1, K1) |
Q0n
→ Q0n+1 |
(J0, K0) |
| 0 |
0 |
0 |
0
| 0 |
0 →
0 |
(0, ×) |
0 →
0 |
(0, ×) |
0 →
0 |
(0, ×) |
0 →
1 |
(1, ×) |
| 1 |
0 | 0 | 0 | 1 |
0 →
0 |
(0, ×) |
0 →
0 |
(0, ×) |
0 →
1 |
(1, ×) |
1 →
0 |
(×, 1) |
| 2 |
0 | 0 | 1 | 0 |
0 →
0 |
(0, ×) |
0 →
0 |
(0, ×) |
1 →
1 |
(×, 0) |
0 →
1 |
(1, ×) |
| 3 |
0 | 0 | 1 | 1 |
0 →
0 |
(0, ×) |
0 →
1 |
(1, ×) |
1 →
0 |
(×, 1) |
1 →
0 |
(×, 1) |
| 4 |
0 | 1 | 0 | 0 |
0 →
0 |
(0, ×) |
1 →
1 |
(×, 0) |
0 →
0 |
(0, ×) |
0 →
1 |
(1, ×) |
| 5 |
0 | 1 | 0 | 1 |
0 →
0 |
(0, ×) |
1 →
1 |
(×, 0) |
0 →
1 |
(1, ×) |
1 →
0 |
(×, 1) |
| 6 |
0 | 1 | 1 | 0 |
0 →
0 |
(0, ×) |
1 →
1 |
(×, 0) |
1 →
1 |
(×, 0) |
0 →
1 |
(1, ×) |
| 7 |
0 | 1 | 1 | 1 |
0 →
1 |
(1, ×) |
1 →
0 |
(×, 1) |
1 →
0 |
(×, 1) |
1 →
0 |
(×, 1) |
| 8 |
1 | 0 | 0 | 0 |
1 →
1 |
(×, 0) |
0 →
0 |
(0, ×) |
0 →
0 |
(0, ×) |
0 →
1 |
(1, ×) |
| 9 |
1 | 0 | 0 | 1 |
1 →
1 |
(×, 0) |
0 →
0 |
(0, ×) |
0 →
1 |
(1, ×) |
1 →
0 |
(×, 1) |
| 10 |
1 | 0 | 1 | 0 |
1 →
0 |
(×, 1) |
0 →
0 |
(0, ×) |
1 →
0 |
(×, 1) |
0 →
0 |
(0, ×) |
(J0, K0)
J
0, K
0 についてカルノー図を使用して論理式を求める.
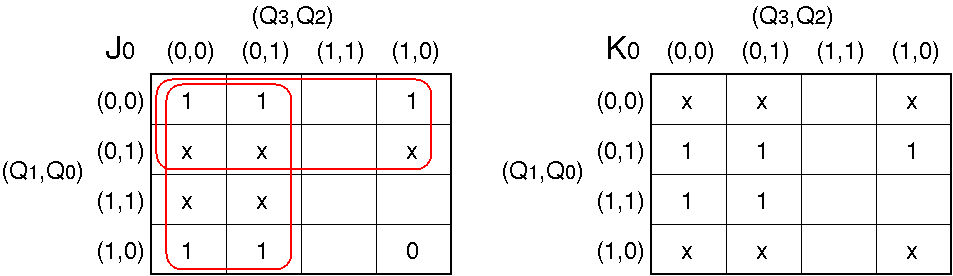
J0 = Q3
+ Q1
= Q3·
Q1
K0 = 1
あるいは
J0 = K0
= Q3·
Q1
(J1, K1)
J
1, K
1 についてカルノー図を使用して論理式を求める.
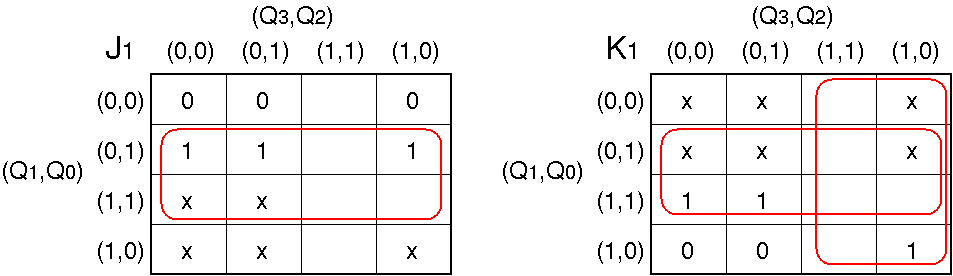
J1 = Q0
K1 = Q3 + Q0
(J2, K2)
J
2, K
2 についてカルノー図を使用して論理式を求める.
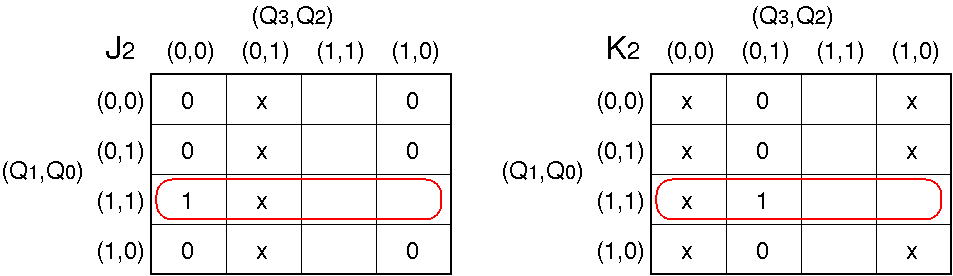
J2 = K2 = Q1·Q0
(J3, K3)
J
3, K
3 についてカルノー図を使用して論理式を求める.
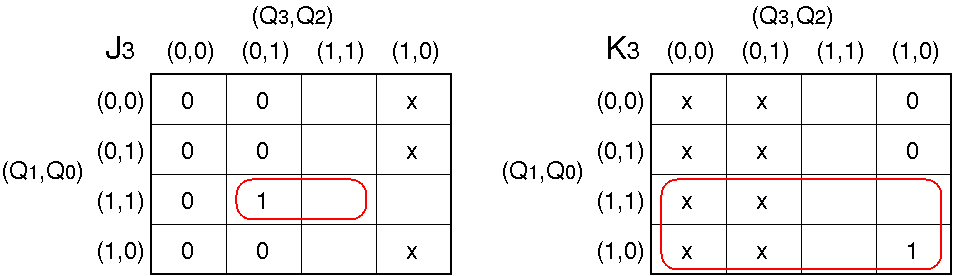
J3 = Q2·Q1·Q0
K3 = Q1
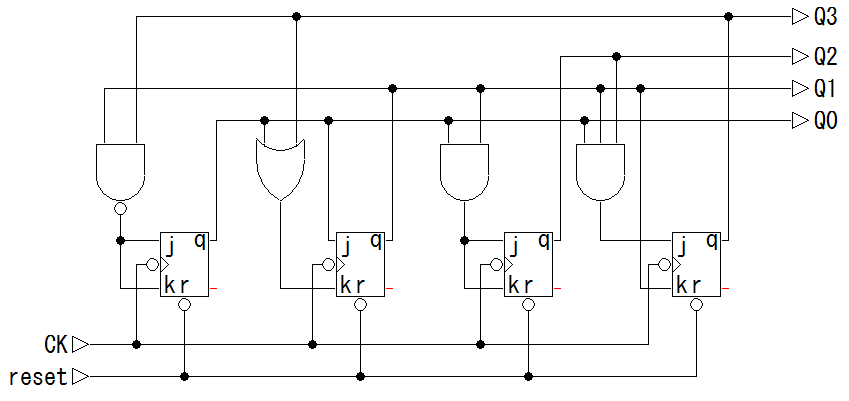
J0 = K0
= Q3·
Q1
J1 = Q0
,
K1 = Q3 + Q0
J2 = K2 = Q1·Q0
J3 = Q2·Q1·Q0
,
K3 = Q1
n進カウンタの設計方針
順序回路をJKフリップフロップを用いて構成し,
組合せ回路の部分を以下の手順により決定する.
- 状態(出力Q)の変化を表にする
- 各状態の変化に対して要求される(J, K)端子への入力信号値を決定する
- カルノー図を利用して,各J, K端子への入力信号の論理式を求める