- 論理ゲート
論理演算を行う電子回路であり,その動作は論理式や真理値表で表すことができる.
- 真理値表
入力のすべての組み合わせと出力の値の組み合わせ表
- 基本論理ゲート
NOT, AND, ORゲートを基本論理ゲートと呼ぶ. これら3種類のゲートを用いることで,任意の論理関数を構成できる.
NOTゲート
否定: Y=A
真理値表
|
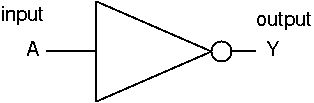 ゲート図 (MIL 論理記号) |
ANDゲート
論理積: Y = A · B
論理積: Y = A · B · C
真理値表
|
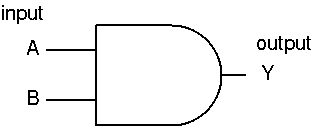 ゲート図 (MIL 論理記号) |
真理値表
|
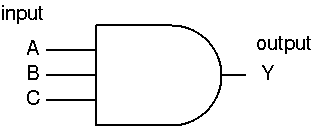 ゲート図 (MIL 論理記号) |
ORゲート
論理和: Y = A + B
論理和: Y = A + B + C
真理値表
|
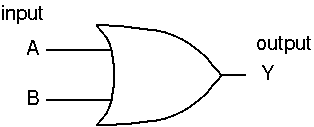 ゲート図 (MIL 論理記号) |
真理値表
|
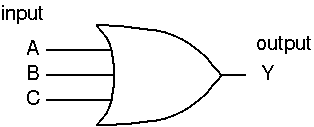 ゲート図 (MIL 論理記号) |
NANDゲート
NAND: Y = A · B
真理値表
|
 ゲート図 (MIL 論理記号) |
NORゲート
NOR: Y = A + B
真理値表
|
 ゲート図 (MIL 論理記号) |
EXORゲート
排他的論理和(exclusive OR): Y = A ⊕ B
真理値表
|
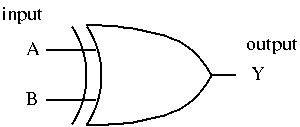 ゲート図 (MIL 論理記号) |
EXNORゲート
ex-nor: Y = A ⊕ B
真理値表
|
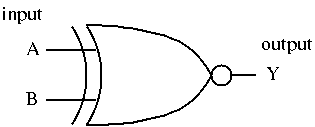 ゲート図 (MIL 論理記号) |
(2) 集合と論理式
集合の考え方を用いれば,論理式の働きを体系的に理解できる.
- 集合,要素
ものの集まりを集合(set)と呼び,集合を構成するものを元(member),あるいは, 要素(element)と呼ぶ.
p が集合Aの要素であることを
p ∈ Aと記述し, pは集合Aに属するという. qが集合Aの要素ではないことをq ∉ Aと表す. - 部分集合
集合Aのすべての要素が集合Bに属するとき,AはBの部分集合であるといい,
A ⊂ Bと表す. - 全体集合
考察対象全体の集合を全体集合(U: universal set)と呼ぶ.
- 補集合
全体集合から集合Aに属する元をすべて取り除いた集合をAの補集合と呼び, A と表す.
- 空集合
要素を1つも持たない集合を空集合(empty set)と呼び, ∅ と表す.
- ベン図(Venn's diagram)
ベン図は平面上の点の集まりによって図的に集合を表すものである.
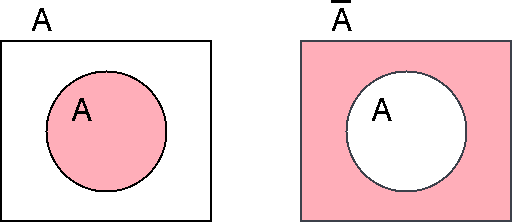
集合と論理式の間には次のような対応関係がある.
和集合
集合Aと集合Bの和集合(union)を A∪B と表す. 記号∪ は「cup」 と読む.
x∈A あるいは x∈B ならば x∈(A∪B)
| 和集合 A ∪ B | 論理和 |
|---|---|
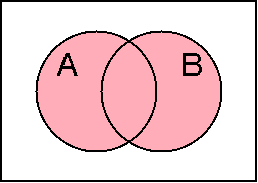 |
A + B |
積集合
集合Aと集合Bの積集合(intersection)を A∩B と表す. 記号∩ は「cap」 と読む.
x∈A かつ x∈B ならば x∈(A∩B)
| 積集合 A ∩ B | 論理積 |
|---|---|
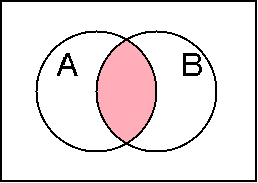 | A · B |
(3) 演算の順序
論理式における演算の順序
- 括弧内
- 否定(NOT)
- 論理積(AND)
- 論理和(OR)
(4) 演習問題
教科書 p. 15 の演習問題を解いてみる.